My research

My research lies at the intersection of multiple fields: statistical physics, macroeconomics, and mathematical optimization. The particular modeling paradigm I employ is Agent-based Modeling. Using both simulations and analytical techniques from statistical physics, in my research I aim to understand the aggregate behavior of the economy with Agent-Based Models.

Agent-based Models

Agent-based models (ABMs) have emerged as a complementary paradigm for modeling macroeconomic phenomena. They provide a flexible framework for understanding the complexity of the macroeconomy while at the same time taking into account the heterogeneous nature of economic actors, institutions, and markets without making overly restrictive assumptions. ABMs take a “bottom-up” approach towards macroeconomic modeling by simulating the behavior of each individual agent in the economy and then aggregating to reveal emergent phenomena such as endogenous business cycles and flash crashes. Using computer simulations, ABMs allow us to model heterogeneities and interactions at any level of detail. Thus they provide a veritable in silico playground for performing economic research. One of the earliest examples of such models in economics is the Schelling Model, which showed how, in the aggregate, segregationist behavior can emerge even without individuals themselves holding segregationist views.

Model for debt dynamics

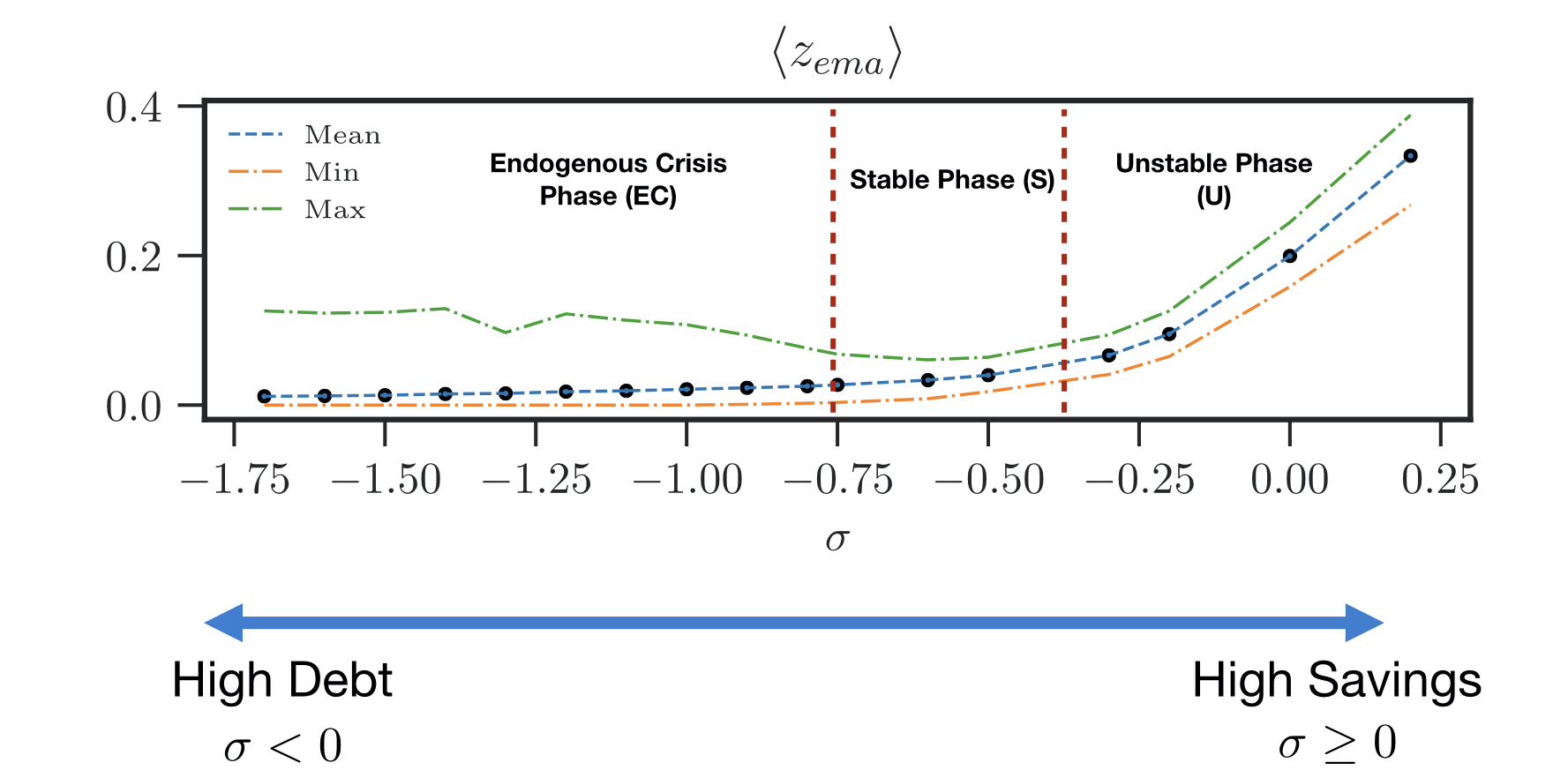
In the first ABM that I developed, I demonstrated how interacting budgetary constraints, when aggregated, couple the production level of the economy to agents’ debt. The agents in this model are firms which exchange goods in a market, with each firm constrained to buy/sell goods as long as they remain within their budgets. The model reveals the existence of three regimes and underscores the importance of debt for macroeconomic stability: at low-levels of debt, the economy remains structure-less with frequent bankruptcies of firms while too high debt leads to endogenous business cycles. Between these two extremes, an intermediate regime of relative stability is found with low levels of bankruptcies for all times. For more details, you can take a look at the paper here.

Reducing model complexity

These regimes have been identified using “phase diagrams”, an important concept in statistical physics. The phase diagram reduces the complexity of the model to a few key parameters with clearly defined macroscopic regimes or ‘phases’. A typical example is the phase-diagram for water exhibiting solid, liquid, and gaseous phases. While microscopically the behavior of individual water molecules might be very complex to study, within each phase there is remarkable regularity. Importantly, the macroscopic properties within these phases are emergent and individual constituents don’t necessarily possess these properties. These phases are delimited by phase boundaries: a system sitting close to such a boundary can become strongly non-linear, with the response to small perturbations becoming rather large. For water, such a tipping point occurs at $0^{\circ}$ C, when a tiny temperature change can drive the system to a completely different macroscopic phase.

Using phase diagrams for studying agent-based models is an important methodological advancement. Macroeconomic ABMs of the type I study aim for understanding modern economies which are complex and inter-connected systems. Consequently, the parameter space of these models is very large and there is the risk of foregoing understanding our models to what Sims has termed “the wilderness of high-dimensional spaces”. My research indicates that by using phase diagrams, we have a systematic way of reducing the parameter space of ABMs to a few key parameters. This helps in building intuition for these models and opens possibilities for them to be used in formulating economic policy.

Economic consequences of Covid

I use the phase diagram in a second model. Here, I have looked at the effect of exogenous consumption and productivity shocks due to the Covid pandemic. Using the phase diagram I identify the parameters of the shock most likely to push the economy towards a state of perennially low output. The ABM paradigm also helps in testing the efficacy of policy proposals, especially those that haven’t previously been tested. This is the case with the hotly debated “helicopter drop”. Under such a proposal, the central bank directly transfers money to citizens which they can spend in the economy. Such a proposal is complimentary to the usual mechanism that central banks use, which is via interest rate cuts or more recently through asset purchases called quantitative easing (QE). I have shown how helicopter money does help in stimulating demand in the economy which does lead to inflation in the long-run which could be a desirable thing given how we are in a deflationary environment in Europe.

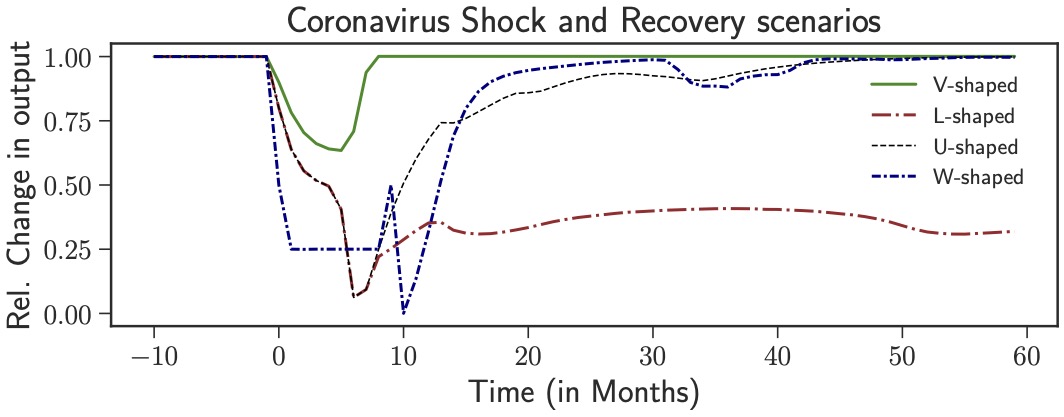
This highlights the importance of ABMs as multi-purpose “scenario generators”, for generating outcomes that are difficult to foresee due to the intrinsic complexity of macro-economic dynamics and also for testing policy proposals without historical antecedents. This work has been published as a preprint and also available at Covid economics.